이번에 배워볼 알고리즘은 합집합 찾기(Union Find) 알고리즘이다. 서로소 집합(Disjoint Set) 알고리즘이라고도 불리는 이 알고리즘은 그래프 상의 두 개의 노드가 같은 그래프에 속하는지를 판별하기 위해 사용되는 알고리즘이다.
다음에 배울 최소 비용 신장 트리(MST)를 구성하는 알고리즘 중 하나인 크루스칼(Kruskal) 알고리즘이 합집합 찾기 알고리즘을 응용한 알고리즘이다.
합집합 찾기 알고리즘의 원리는 다음과 같다.
- 자신의 부모 노드를 저장하는 1차원 배열을 선언 후 각 정점의 부모를 자신을 가리키도록 초기화한다.
- 두 개의 노드를 선택하여 Union 연산을 수행하면 두 개의 노드의 부모를 하나의 노드로 통일한다. 이때 더 작은 번호를 가리키도록 부모를 통일한다.
- 두 개의 노드를 선택하여 Find 연산을 수행하면 두 개의 노드가 같은 그래프인지를 판별한다. 만약 같은 부모를 가리킨다면 같은 그래프에 속한 것이고, 다른 부모를 가리킨다면 서로 다른 그래프에 속한 것이다.
그렇다면 합집합 찾기 알고리즘이 어떤 식으로 동작하는지 살펴보자.

위 그림과 같이 총 7개의 정점이 존재한다고 하자. 현재 모든 정점들은 서로 연결되지 않았기 때문에 자신을 부모로 가리키도록 초기 상태를 설정한다.

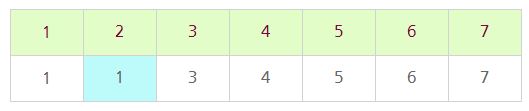
만약 1번 정점과 2번 정점을 연결하면 어떻게 될까?

우리는 1번 정점과 2번 정점이 연결되었다는 것을 알 수 있지만 컴퓨터의 입장에서는 알 수가 없다. 이를 위해 우리는 부모의 번호를 가리키는 1차원 배열을 사용하기로 하였다.
두 개의 정점이 가리키고 있는 현재 부모의 번호 중 큰 번호를 가지는 정점을 작은 번호로 변경한다. 따라서 2번 정점은 1번 정점을 부모로 가리키도록 한다. 이것이 바로 Union 연산이다.
이번에는 2번과 6번 정점, 4번과 7번 정점을 연결해보자.

2번 정점은 현재 1번 정점을 가리키고 있고 6번 정점은 현재 자신을 가리키고 있다. Union 연산을 통해 6번 정점의 부모를 2번 정점의 부모인 1번 정점을 가리키도록 한다.
이때 6번 정점의 부모를 그냥 2번 정점을 가리키도록 할 수도 있다. 하지만 이렇게 한다면 우리는 1번 정점과 6번 정점이 서로 연결되었다는 것을 알 수 있지만 컴퓨터의 입장에서는 서로 다른 번호를 가리키고 있기 때문에 알 수가 없다.
알기 위해선 6번의 부모를 호출(2), 또다시 6번의 부모(2)의 부모를 호출(1), 이런 식으로 부모의 정점을 계속 호출하면서 1번 정점이 가리키는 번호가 나올 때까지 연산을 수행해야 하는데 이는 굉장히 비효율적이다.
이를 해결하기 위해 부모를 가장 낮은 번호로 가리키도록 하는 것이다. 마찬가지로 7번 정점의 부모를 4번 정점을 가리키도록 한다.

이번에는 2번과 3번 정점, 5번과 7번 정점을 연결해보자.

Union 연산을 통해 3번 정점의 부모를 2번 정점이 가리키는 부모인 1번 정점을 가리키도록 하고, 5번 정점의 부모를 7번 정점의 가리키는 부모인 4번 정점을 가리키도록 한다.
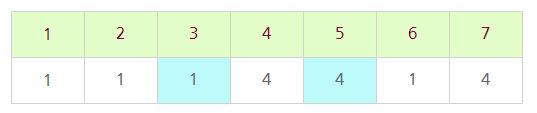
그렇다면 이번에는 두 개의 정점이 같은 부모에 속하는지를 판별해보기 위해 1번 정점과 6번 정점을 선택하여 Find 연산을 수행해보자.
1번 정점과 6번 정점은 서로 같은 부모인 1번 정점을 가리키고 있기 때문에 두 개의 정점은 같은 그래프에 속한다고 알 수 있다. 이와 반대로 3번 정점과 5번 정점을 Find 연산을 수행하면 3번 정점은 1번 정점을 가리키고 5번 정점은 4번 정점을 가리키기 때문에 서로 다른 그래프에 속한다고 알 수 있다.
합집합 찾기 알고리즘을 Java로 구현한 코드는 다음과 같다.
class Union_Find {
int vertexCnt;
int[] parent;
public Union_Find(int N) {
this.vertexCnt = N;
parent = new int[N + 1];
// 모든 정점의 부모는 자신을 가리키도록 초기화
for (int i = 0; i <= N; ++i) {
parent[i] = i;
}
}
public void union(int v1, int v2) {
//두 노드의 부모 노드를 호출
v1 = getParent(v1);
v2 = getParent(v2);
if (v1 == v2) return;
//부모 노드의 번호가 큰 노드를 작은 번호를 가리키도록 변경
if (v1 > v2) {
parent[v1] = v2;
} else {
parent[v2] = v1;
}
}
public int getParent(int v) {
//만약 v와 v가 가리키는 부모의 정점이 같다면
if (parent[v] == v) return v;
//다르다면 자신의 부모의 부모를 호출
//호출된 값을 parent[v]에 저장함으로써 항상 작은 번호의 부모를 가리키도록 함
return parent[v] = getParent(parent[v]);
}
public boolean find(int v1, int v2) {
v1 = getParent(v1);
v2 = getParent(v2);
if (v1 == v2) return true;
return false;
}
public void print_Parent() {
for (int i = 1; i <= vertexCnt; ++i) {
System.out.println("Parent of [" + i + "] is " + parent[i]);
}
}
}
public class Blog {
public static void main(String[] args) {
Union_Find uf = new Union_Find(7);
uf.union(1, 2);
uf.union(2, 6);
uf.union(4, 7);
uf.union(2, 3);
uf.union(5, 7);
uf.print_Parent();
System.out.println(uf.find(1, 6));
System.out.println(uf.find(3, 5));
}
}'Computer Science > 알고리즘' 카테고리의 다른 글
| 프림 알고리즘(Prim Algorithm) (0) | 2021.07.04 |
|---|---|
| 크루스칼 알고리즘(Kruskal Algorithm) (0) | 2021.07.04 |
| 플로이드-워셜 알고리즘(Floyd-Warshall Algorithm) (0) | 2021.07.03 |
| 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2021.07.03 |
| 다익스트라 알고리즘(Dijkstra Algorith) (0) | 2021.07.03 |




댓글