이번에 배워볼 알고리즘은 크루스칼 알고리즘(Kruskal Algorithm)과 같이 최소 비용 신장 트리(MST)를 구하는 프림 알고리즘(Prim Algorithm)이다.
크루스칼 알고리즘은 간선 선택을 기반으로 하는 알고리즘이었다면, 프림 알고리즘은 정점 선택을 기반으로 하는 알고리즘이다. 또한, 크루스칼 알고리즘은 이전 단계에서 만들어진 신장 트리와는 상관없이 무조건 최소 간선만을 선택하는 방법이라면, 프림 알고리즘은 이전 단계에서 만들어진 신장 트리를 확장하는 방식이다.
프림 알고리즘은 그리디 알고리즘에 속한다. 그 이유는 추가할 새로운 정점을 선택할 때 최소 비용을 가지는 간선을 선택하기 때문이다.
프림 알고리즘의 동작 원리는 다음과 같다.
- 시작 정점을 선택한다.
- 현재 구성된 신장 트리에 속한 정점과 속하지 않은 정점들 사이의 간선들 중 최소 가중치를 갖는 간선을 선택하여 정점을 연결한다.
위 과정을 모든 정점이 연결될 때까지 진행한다. 그렇다면 프림 알고리즘의 동작 과정을 그림으로 살펴보자.
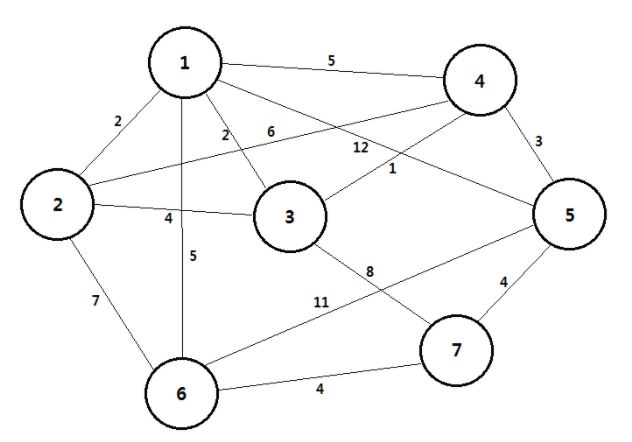
위 그림과 같은 가중치를 가지는 무방향 그래프가 있다고 하자. 나는 시작 정점을 1번 정점으로 선택하겠다. 1번 정점에 연결된 간선들 중에 최소 신장 트리를 구성하지 않는 정점과 연결된 간선들을 리스트에 담아준다.

리스트에서 최소 비용을 가지는 간선을 선택한다. 2번 정점은 최소 신장 트리에 속하지 않기 때문에 2의 비용을 가지고 1번 정점과 2번 정점을 연결해 주는 간선을 선택하고 연결해 준다. 또한 최소 신장 트리에 속하지 않은 정점 중 2번 정점과 연결된 간선을 담아준다.

리스트에서 최소 비용을 가지는 간선을 선택한다. 3번 정점은 최소 신장 트리에 속하지 않기 때문에 2의 비용을 가지고 1번 정점과 3번 정점을 연결해 주는 간선을 선택하고 연결해 준다. 또한 최소 신장 트리에 속하지 않은 정점 중 3번 정점과 연결된 간선을 담아준다.
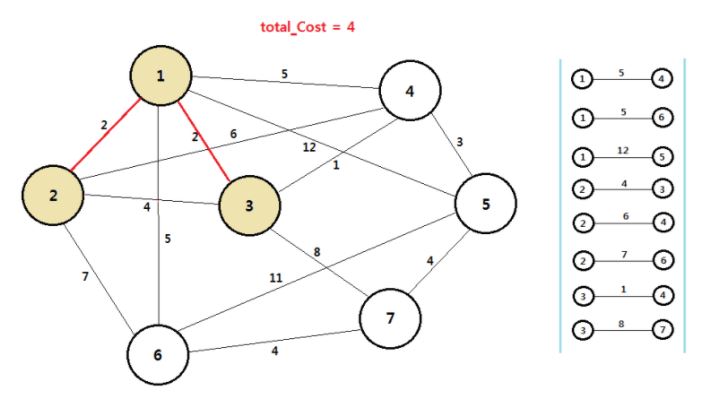
리스트에서 최소 비용을 가지는 간선을 선택한다. 4번 정점은 최소 신장 트리에 속하지 않기 때문에 1의 비용을 가지고 3번 정점과 4번 정점을 연결해 주는 간선을 선택하고 연결해 준다. 또한 최소 신장 트리에 속하지 않은 정점 중 4번 정점과 연결된 간선을 담아준다.
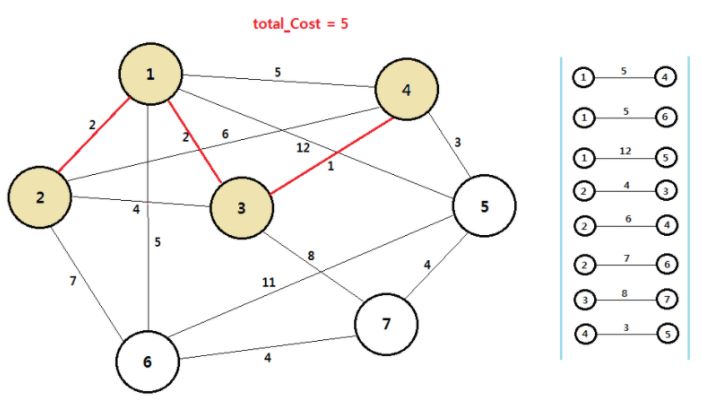
리스트에서 최소 비용을 가지는 간선을 선택한다. 5번 정점은 최소 신장 트리에 속하지 않기 때문에 3의 비용을 가지고 4번 정점과 5번 정점을 연결해 주는 간선을 선택하고 연결해 준다. 또한 최소 신장 트리에 속하지 않은 정점 중 5번 정점과 연결된 간선을 담아준다.

리스트에서 최소 비용을 가지는 간선을 선택한다. 2번 정점과 3번 정점 모두 최소 신장 트리에 속하는 정점이기 때문에 4의 비용을 가지며 2번 정점과 3번 정점을 이어주는 간선은 선택하지 않는다.
다시 한번 리스트에서 최소 비용을 가지는 간선을 선택한다. 7번 정점은 최소 신장 트리에 속하지 않기 때문에 4의 비용을 가지고 5번 정점과 7번 정점을 연결해 주는 간선을 선택하고 연결해 준다. 또한 최소 신장 트리에 속하지 않은 정점 중 7번 정점과 연결된 간선을 담아준다.
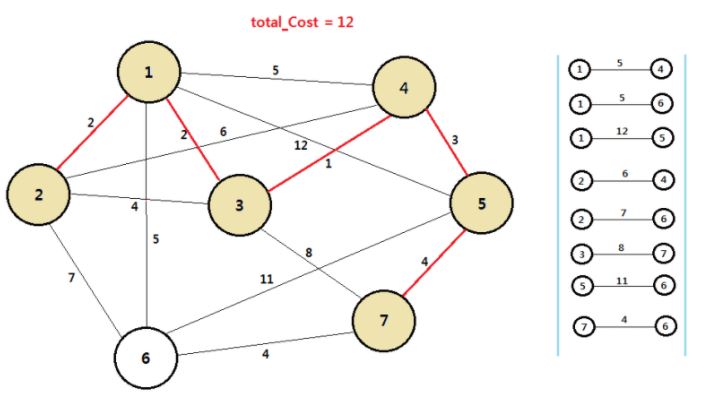
리스트에서 최소 비용을 가지는 간선을 선택한다. 6번 정점은 최소 신장 트리에 속하지 않기 때문에 4의 비용을 가지고 7번 정점과 6번 정점을 연결해 주는 간선을 선택하고 연결해 준다. 모든 정점이 연결되었기 때문에 종료한다.

최종 결과는 이전 크루스칼 알고리즘으로 구성한 MST와 동일하다. 물론 최종 결과가 다를 수도 있다. 그 이유는 그래프에서 MST의 개수가 1개 이상일 수가 있기 때문이다. 상황에 따라 다른 형태의 MST가 구성될 수도 있다. 하지만 결국 구성하는데 드는 최종 비용은 동일할 것이다.
프림 알고리즘의 동작 과정을 살펴보면 결국 최소 신장 트리에 속하지 않은 정점들과 연결해 주는 간선들 중 최소 비용을 가지는 간선을 뽑는 것이 시간 복잡도를 좌우한다.
리스트를 배열로 구현한다면 리스트 내의 모든 간선 중 최소비용을 가지는 간선을 찾기 위해선 순차적으로 탐색해야 하기 때문에 O(V^2)의 시간 복잡도를 가지게 된다.
하지만 간선들을 우선순위 큐로 관리한다면 O(E logV)라는 시간 복잡도를 가지는 프림 알고리즘으로 개선할 수 있다.
따라서 간선이 적은 희소 그래프인 경우 크루스칼 알고리즘이 적합하고 간선이 많은 밀집 그래프인 경우 프림 알고리즘이 적합하다.
간선을 관리하는 리스트를 배열로 구현한 프림 알고리즘은 다음과 같다.
import java.util.Arrays;
class MyGraph {
final int INF = 987654321;
int vertexCnt;
int[][] m;
int[] dist;
boolean[] selected;
public class Edge implements Comparable<Edge>{
int from, to, cost;
public Edge(int from, int to, int cost) {
this.from = from;
this.to = to;
this.cost = cost;
}
@Override
public int compareTo(Edge o) {
return this.cost - o.cost;
}
}
public MyGraph(int N) {
this.vertexCnt = N;
m = new int[N+1][N+1];
}
public void insert_Edge(int from, int to, int cost) {
m[from][to] = cost;
m[to][from] = cost;
}
public int prim_Array(int start) {
//자기 자신을 제외한 갈수없는 경로는 INF로 초기화
for (int i = 1; i <= vertexCnt; ++i) {
for (int j = 1; j <= vertexCnt; ++j) {
if (i == j) continue;
if (m[i][j] == 0) m[i][j] = INF;
}
}
int total_Cost = 0;
selected = new boolean[vertexCnt+1]; //최소 신장 트리에 속한 정점
dist = new int[vertexCnt+1]; //현재 구성된 최소 신장 트리에서 각 정점에 대한 비용
Arrays.fill(dist, INF);
dist[start] = 0;
//정점의 횟수만큼 돌면서
for (int i = 1; i <= vertexCnt; ++i) {
int v = get_Min_Vertex(); //dist 배열에서 최소 값을 가지는 정점
selected[v] = true;
if (dist[v] == INF) return INF; //연결할 수 있는 경로가 없다면 종료
total_Cost += dist[v];
//dist 배열 갱신
for (int j = 1; j <= vertexCnt; ++j) {
if (!selected[j] && dist[j] > m[v][j]) {
dist[j] = m[v][j];
}
}
}
return total_Cost;
}
public int get_Min_Vertex() {
int v = -1;
int min = INF;
for (int i = 1; i <= vertexCnt; ++i) {
if (!selected[i] && min > dist[i]) {
v = i;
min = dist[i];
}
}
return v;
}
}
public class Blog {
public static void main(String[] args) {
MyGraph mg = new MyGraph(7);
mg.insert_Edge(1, 2, 2);
mg.insert_Edge(1, 3, 2);
mg.insert_Edge(1, 4, 5);
mg.insert_Edge(1, 5, 12);
mg.insert_Edge(1, 6, 5);
mg.insert_Edge(2, 3, 4);
mg.insert_Edge(2, 4, 6);
mg.insert_Edge(2, 6, 7);
mg.insert_Edge(3, 4, 1);
mg.insert_Edge(3, 7, 8);
mg.insert_Edge(4, 5, 3);
mg.insert_Edge(5, 6, 11);
mg.insert_Edge(5, 7, 4);
mg.insert_Edge(6, 7, 4);
System.out.println(mg.prim_Array(1));
}
}
간선을 관리하는 리스트를 우선순위 큐로 구현한 프림 알고리즘은 다음과 같다.
import java.util.ArrayList;
import java.util.PriorityQueue;
class MyGraph {
final int INF = 987654321;
int vertexCnt;
ArrayList<Edge>[] edge_List;
boolean[] selected;
public class Edge implements Comparable<Edge>{
int to, cost;
public Edge(int to, int cost) {
this.to = to;
this.cost = cost;
}
@Override
public int compareTo(Edge o) {
return this.cost - o.cost;
}
}
public MyGraph(int N) {
this.vertexCnt = N;
edge_List = new ArrayList[N+1];
for (int i = 0; i <= N; ++i) {
edge_List[i] = new ArrayList<>();
}
}
public void insert_Edge(int from, int to, int cost) {
edge_List[from].add(new Edge(to, cost));
edge_List[to].add(new Edge(from, cost));
}
public int prim_PQ(int start) {
int total_Cost = 0;
selected = new boolean[vertexCnt+1]; //최소 신장 트리에 속한 정점
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.offer(new Edge(start, 0)); //0의 비용을 가지는 시작점을 넣어줌
//정점의 횟수만큼 돌면서
for (int i = 1; i <= vertexCnt; ++i) {
int v = -1;
int min = INF;
//간선들중에 최소 비용 신장 트리에 속하지 않고 가장 적은 비용을 가지는 정점을 뽑음
while (!pq.isEmpty()) {
Edge e = pq.poll();
if (!selected[e.to]) {
v = e.to;
min = e.cost;
break;
}
}
//최소 거리가 INF이면 갈수가 없기에 종료
if (min == INF) return INF;
total_Cost += min;
selected[v] = true;
//새로 추가한 정점에 인접하고 최소 비용 신장 트리에 속하지는 않은 정점으로 가는 간선들을 우선순위 큐에 넣어줌
for (int j = 0; j < edge_List[v].size(); ++j) {
Edge e = edge_List[v].get(j);
if (!selected[e.to]) {
pq.offer(e);
}
}
}
return total_Cost;
}
}
public class Blog {
public static void main(String[] args) {
MyGraph mg = new MyGraph(7);
mg.insert_Edge(1, 2, 2);
mg.insert_Edge(1, 3, 2);
mg.insert_Edge(1, 4, 5);
mg.insert_Edge(1, 5, 12);
mg.insert_Edge(1, 6, 5);
mg.insert_Edge(2, 3, 4);
mg.insert_Edge(2, 4, 6);
mg.insert_Edge(2, 6, 7);
mg.insert_Edge(3, 4, 1);
mg.insert_Edge(3, 7, 8);
mg.insert_Edge(4, 5, 3);
mg.insert_Edge(5, 6, 11);
mg.insert_Edge(5, 7, 4);
mg.insert_Edge(6, 7, 4);
System.out.println(mg.prim_PQ(1));
}
}'Computer Science > 알고리즘' 카테고리의 다른 글
| 다이나믹 프로그래밍(Dynamic Programming) : 동적계획법 (0) | 2021.07.04 |
|---|---|
| 위상 정렬(Topological Sort) (0) | 2021.07.04 |
| 크루스칼 알고리즘(Kruskal Algorithm) (0) | 2021.07.04 |
| 합집합 찾기(Union Find) (0) | 2021.07.03 |
| 플로이드-워셜 알고리즘(Floyd-Warshall Algorithm) (0) | 2021.07.03 |




댓글