이번에 배워볼 알고리즘은 플로이드-워셜 알고리즘(Floyd-Warshall Algorithm)이다. 이전에 배운 다익스트라, 벨만-포드 알고리즘은 한 정점에서 다른 정점으로 가는 최단 경로를 구하는 알고리즘이었다면, 플로이드-워셜은 모든 정점에서 모든 정점으로의 최단 경로를 구하는 알고리즘이다.
플로이드 워셜 알고리즘은 벨만-포드 알고리즘처럼 음의 간선이 존재하여도 모든 최단 경로를 구할 수 있다. 물론 음의 사이클이 존재하면 불가능하다.
또한, 이전에 저장해놓은 최단 경로를 이용해서 새로운 최단 경로로 갱신하는 과정에서 플로이드 워셜 알고리즘 역시 다이나믹 프로그래밍이라고 할 수 있다.
플로이드 워셜 알고리즘의 핵심은 간단하다. 이전에 다익스트라나 벨만 포드 알고리즘에서 정점 A에서 정점 C까지 가는 경로를 갱신하는 과정을 생각해 보자. 정점 A에서 정점 C까지 가는 비용보다 정점 A에서 다른 정점 B를 거쳐서 정점 C까지 가는 비용이 저렴하다면 갱신하였다.

이처럼 모든 정점에서 모든 정점을 거쳐서 모든 정점으로 가는 경로를 갱신해 주면 된다.
플로이드 워셜 알고리즘의 동작 원리는 다음과 같다.
- 중간에 거쳐가는 기준이 될 정점 k를 선택한다.
- 모든 정점에서 정점 k를 거쳐서 모든 정점으로 가는 비용을 갱신한다. 갱신하는 기준은 위에서 살펴본 것처럼 특정한 정점 A에서 정점 B까지 가는 비용보다 정점 A에서 정점 K를 거쳐 정점 C까지 가는 비용이 저렴하다면 갱신해 준다.
D[i][j] = min(D[i][j], D[i][k] + D[k][j])
// D[i][j] : i번 정점에서 j번 정점까지 가는 최소 비용
// 매번 새로운 비용을 구하는 것이 아니라 이미 저장된 최소 비용을 이용하기 때문에 dp라고 불림
이 과정을 모든 정점에 대해 진행하면 된다. 플로이드 워셜 알고리즘의 동작 과정을 그림으로 알아보자.
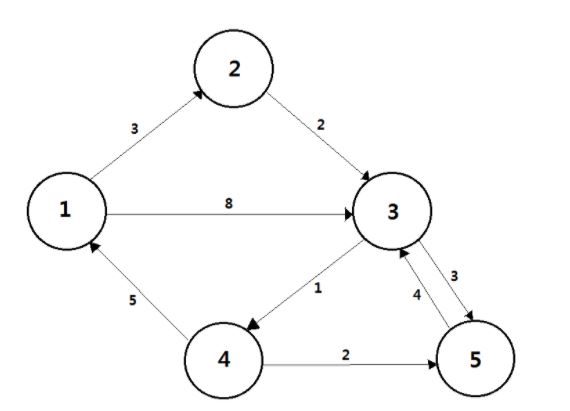
가중치를 가지는 방향 그래프가 위 그림처럼 있다고 하자. 모든 정점의 최단 경로를 구해야 하기 때문에 2차원 배열로 표현한다. D[i][j]는 i 번 정점에서 j 번 정점으로 가는 최소 비용이다. 자신에게 가는 비용은 0, 1개의 간선을 거쳐서 갈 수 있는 경로는 가중치, 나머지는 INF로 초기 상태를 설정한다.

1번 정점을 중간 경로인 기준 정점으로 정하고 모든 정점에서 1번 정점을 거쳐 모든 정점으로 가는 비용을 갱신해 준다. 4-2로 가는 비용 INF보다 4-1-2로 가는 비용 8이 저렴하기 때문에 갱신된다. 4-3으로 가는 비용 INF보다 4-1-3으로 가는 비용 13이 저렴하기 때문에 갱신된다.

2번 정점을 중간 경로인 기준 정점으로 정하고 모든 정점에서 2번 정점을 거쳐 모든 정점으로 가는 비용을 갱신해 준다. 1-3으로 가는 비용 8보다 1-2-3으로 가는 비용 5가 저렴하기 때문에 갱신된다. 4-3으로 가는 비용 13보다 4-2-3으로 가는 비용이 10으로 저렴하기 때문에 갱신된다.

3번 정점을 중간 경로인 기준 정점으로 정하고 위와 같은 방법으로 모든 정점에 대해 갱신해 준다.

4번 정점을 중간 경로인 기준 정점으로 정하고 위와 같은 방법으로 모든 정점에 대해 갱신해 준다.
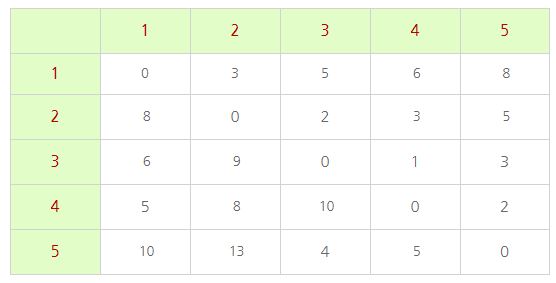
5번 정점을 중간 경로인 기준 정점으로 정하고 위와 같은 방법으로 모든 정점에 대해 갱신해 준다. 정점의 수만큼 반복하여 최종적으로 모든 정점으로 가는 최소 비용을 구하였다.
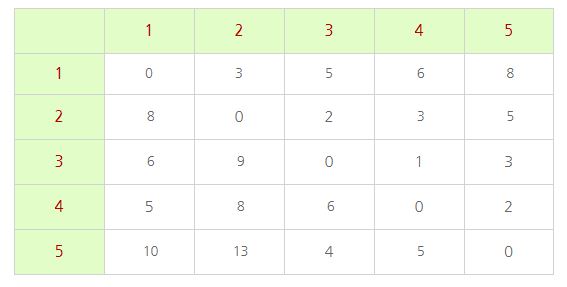
모든 정점에 대해 모든 정점을 거쳐 모든 정점으로 가는 비용을 비교하기 때문에 플로이드 워셜 알고리즘은 O(V^3)의 시간 복잡도를 가진다. 플로이드 워셜 알고리즘은 시간 복잡도가 큰 대신 구현하기가 정말 간단한 장점이 있다.
플로이드 워셜 알고리즘을 Java로 구현한 코드는 다음과 같다.
class MyGraph {
final int INF = 987654321;
int vertexCnt;
int[][] m;
public MyGraph(int N) {
vertexCnt = N;
m = new int[N+1][N+1];
}
public void make_DirectedEdge(int from, int to, int cost) {
m[from][to] = cost;
}
public void floyd_Warshall() {
int[][] dist = new int[vertexCnt+1][vertexCnt+1];
for (int i = 1; i <= vertexCnt; ++i) {
for (int j = 1; j <= vertexCnt; ++j) {
if (i == j) continue;
dist[i][j] = m[i][j] == 0 ? INF : m[i][j];
}
}
for (int k = 1; k <= vertexCnt; ++k) {
for (int i = 1; i <= vertexCnt; ++i) {
for (int j = 1; j <= vertexCnt; ++j) {
if (dist[i][j] > dist[i][k] + dist[k][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
for (int i = 1; i <= vertexCnt; ++i) {
for (int j = 1; j <= vertexCnt; ++j) {
System.out.print(dist[i][j]==INF?"INF ":dist[i][j]+" ");
}System.out.println();
}System.out.println();
}
}
public class Blog {
public static void main(String[] args) {
MyGraph mg = new MyGraph(5);
mg.make_DirectedEdge(1, 2, 3);
mg.make_DirectedEdge(1, 3, 8);
mg.make_DirectedEdge(2, 3, 2);
mg.make_DirectedEdge(3, 4, 1);
mg.make_DirectedEdge(3, 5, 3);
mg.make_DirectedEdge(4, 1, 5);
mg.make_DirectedEdge(4, 5, 2);
mg.make_DirectedEdge(5, 3, 4);
mg.floyd_Warshall();
}
}'Computer Science > 알고리즘' 카테고리의 다른 글
| 크루스칼 알고리즘(Kruskal Algorithm) (0) | 2021.07.04 |
|---|---|
| 합집합 찾기(Union Find) (0) | 2021.07.03 |
| 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2021.07.03 |
| 다익스트라 알고리즘(Dijkstra Algorith) (0) | 2021.07.03 |
| 너비 우선 탐색(Breadth First Search) : BFS (0) | 2021.07.02 |




댓글