이번에 배워볼 자료구조는 세그먼트 트리(Segement Tree)이다. 최근 코딩 테스트에서 세그먼트 트리를 알고 있다면 조금 더 쉽게 해결할 수 있는 문제들이 나오고 있어서 한번 다뤄보려 한다. 세그먼트 트리는 이해하고 구현하는데 난이도가 상당히 있으며, 아직까지는 굳이 몰라도 된다고 생각하기 때문에 보다가 이해가 안 된다면 과감하게 버리는 것을 추천한다.
세그먼트 트리는 트라이처럼 트리를 활용한 자료구조이다. 세그먼트 트리를 이해하기 위해 사용되는 구간 합 구하기라는 대표적인 문제가 있다. 이 문제를 통해 세그먼트 트리를 이해해 보자.
구간 합 구하기 문제는 N 개의 숫자가 나열돼있을 때 a~b 구간 데이터들의 합을 구하는 문제이다. 구간 합을 구하는 방법은 대표적으로 3가지가 존재한다.
첫 번째는 단순하게 a부터 b까지 for 문을 돌리며 각 인덱스의 데이터를 전부 더해서 구하는 방법이다. 이 방법은 단순한 만큼 매번 O(N)의 시간만큼 연산해야 하기 때문에 상당히 비효율적인 방법이다.
두 번째는 누적합을 미리 구해서 저장해놓고 필요할 때 사용하는 방법으로 다이나믹 프로그래밍 기법을 사용한다. 다음과 같이 1차원 배열을 선언하자.
dp[i] : 첫번째 데이터부터 i번째 데이터까지의 누적합우리는 다음과 같은 전처리 과정을 통해 dp[1]부터 dp[N]까지의 누적합을 O(N)의 시간으로 구할 수 있다.
for (int i = 1; i <= N; ++i){
dp[i] = dp[i - 1] + num[i];
}이후 a부터 b까지의 구간 합을 구한다면 dp[b] - dp[a - 1], O(1)의 시간 만에 구할 수 있게 된다.
세 번째 방법은 지금부터 배울 세그먼트 트리를 이용하는 방법이다. 이미 누적합을 이용하는 방법을 통해 전처리 O(N) + 쿼리문 * O(1)의 시간 만에 구간 합을 구할 수 있는데 세그먼트 트리가 왜 필요할까? 다음과 같은 상황을 생각해 보자.
{1, 3, 5, 6, 8, 2, 6, 11}을 가지는 리스트가 있다고 하자. 우리는 누적합을 미리 구해서 빠른 시간 안에 구간 합을 구할 수 있었다.
그런데 만약 5번째 데이터 8을 5로 변경한 후 3~5까지의 구간 합을 구한다면 어떻게 될까? 데이터가 변경이 되면 기존에 구해놓은 누적합 dp 배열을 사용할 수가 없다. 5번째 데이터가 변경되었기 때문에 dp[5]부터 dp[N]까지의 누적합을 새롭게 갱신해 줘야 한다.
매번 데이터의 값이 변경될 때마다 우리는 새롭게 누적합을 갱신해 줘야 하기 때문에 O(N)의 시간이 걸린다. 하지만 세그먼트 트리를 이용한다면 데이터의 값이 변경되어도 O(log N)의 시간 만에 갱신 및 구간 합을 구할 수 있다.
균형 잡힌 트리의 특성상 모든 노드들을 트리의 높이, O(log N)의 시간 안에 접근할 수 있다. 이를 활용해서 데이터가 변경이 되어도 O(log N)의 시간 만에 데이터 및 데이터를 포함하는 구간 합을 업데이트해 주는 것이 세그먼트 트리의 특징이다.
세그먼트 트리의 형태는 다음과 같다. 최말단 노드에는 각 인덱스의 데이터를 삽입해 준다. 그 후 상위 노드로 올라갈 때마다 자식들의 누적합을 저장해놓는다.

만약 1~6까지의 구간 합을 구한다면 어떻게 하면 될까? 루트 노드에서 시작하여 내려가면서 노드에 저장된 누적합 구간이 구하고자 하는 구간에 속한다면 더 이상 내려갈 필요 없이 저장된 값을 반환해주면 된다.
좌측의 경우 1~4구간이 구하고자 하는 구간에 속하기 때문에 더 이상 내려가지 않는다. 우측의 경우 5~8은 구하고자 하는 구간을 넘기 때문에 좌측으로 내려가 주며, 5~6구간은 구하고자 하는 구간에 속하기 때문에 더 이상 내려갈 필요 없이 저장된 값을 반환한다.
우리는 O(log N) 시간 만에 해당 구간 합을 구하였다. 사실 데이터의 변경이 없이 여러번 구간 합을 구한다면 두 번째 방법인 누적합으로 구하는 것이 더 효율적이다.

그렇다면 세그먼트 트리의 장점을 알기 위해 5번째 데이터인 8을 3으로 변경해보자. 누적합을 이용했다면 새롭게 dp 값을 경신해줘야 했기 때문에 O(N)의 시간이 들었다.
하지만 세그먼트 트리를 이용한다면 5를 포함하는 구간의 노드들만 갱신해주면 된다. 1~4구간은 5구간을 포함하지 않기 때문에 갱신할 필요가 없으며, 5구간을 포함하는 5, 5~6, 5~8, 1~8구간 순서로 4개의 노드만 갱신해주면 된다. 균형 잡힌 트리의 특성상 O(log N)의 시간만에 갱신할 수 있게 된다.

대충 세그먼트 트리가 어떤 것인지 파악했을 것이다. 그렇다면 구현으로 넘어가 보자.
세그먼트 트리를 구현하는 방법은 반복문을 이용한 Bottom-Up 방식과 재귀 함수를 이용한 Top-Down 방식이 있다. 반복문을 이용한 방법은 재귀 함수를 이용한 방법보다 구현하기가 쉽고 속도도 빠르다. 이에 반해 재귀 함수를 이용한 방법은 확장성이 뛰어나다는 장점이 있다. 따라서 상황에 따라 적절히 사용하는 것을 추천한다.
먼저 반복문을 이용한 Bottom-Up 방식을 알아보자.
세그먼트 트리 형태를 보면 완전 이진 트리의 형태인 것을 알 수 있다. 이전에 배운 힙 자료구조를 한번 생각해 보자.
자식의 인덱스는 부모의 인덱스 * 2, 부모의 인덱스 * 2 + 1로 접근할 수 있었다. 반대로 부모의 인덱스는 자식의 인덱스 / 2로 접근할 수 있었다. 이를 활용해서 최말단 노드(Bottom)부터 최상단 노드(Up)까지 차례대로 값을 더해주면서 갱신해 주면 된다.
그렇다면 먼저 트리의 전체 구조를 설정해야 한다.
먼저 최말단 노드의 인덱스는 어떻게 구할까? 루트 노드의 인덱스를 1로 둔다면 각 높이의 첫 번째 노드는 1, 2, 4, 8... 의 형태로 2^(높이 - 1)인 것을 알 수가 있다. 따라서 최말단 노드의 첫 번째 인덱스는 다음과 같다.

그렇다면 트리의 높이는 어떻게 될까? 높이에 따른 최말단 노드 개수는 1, 2, 4, 8...로 2의 제곱수 형태를 갖는다. N개의 데이터를 차례대로 넣기 위해 최말단 노드의 개수는 N보다 크거나 같아야 한다. 따라서 트리의 높이는 다음과 같다. ceil는 올림 함수이다.

마지막으로 트리의 크기는 어떻게 될까? 세그먼트 트리는 N개의 데이터를 넣기 위한 N개의 최말단 노드들이 필요하다. 트리의 높이에 따라 최말단 노드의 개수는 1, 2, 4, 8...의 형태로 2^(높이-1)인 것을 알 수 있다.
완전 이진트리는 최말단 노드를 제외한 노드들의 개수는 최말단 노드의 개수 - 1이다. 또한, 우리는 1번 인덱스부터 사용하기 위해 트리의 크기는 다음과 같다.

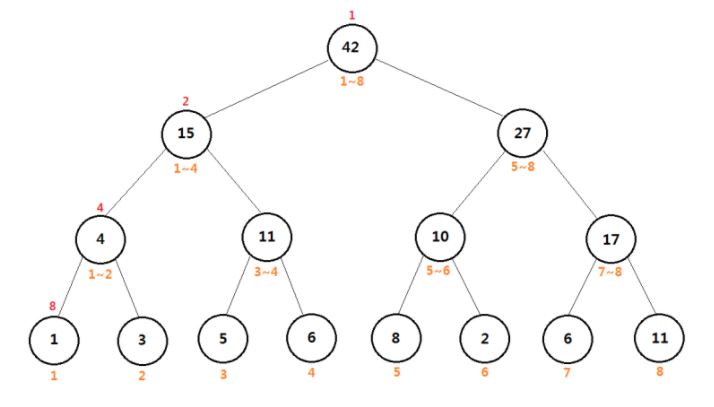
트리의 전체 구조를 설정했다면 반복문을 통해 N개의 데이터를 최말단 노드부터 삽입해 주면 된다. 최말단 노드의 첫 번째 인덱스를 구했기 때문에 N번째 데이터의 인덱스는 최말단 노드의 첫 번째 인덱스 + (N - 1)이다. 최말단 노드에 N번째 데이터를 삽입한 후 부모 노드로 올라가면서 자신의 값을 더해주면 된다.
그렇다면 N 번째 데이터를 변경한다면 어떻게 될까? 간단하다. N번째 데이터의 최말단 노드의 첫 번째 인덱스 + (N - 1)의 값을 변경해 주고 루트 노드까지 올라가면서 갱신해 주면 된다. 결국 위의 삽입 과정과 동일한 방법으로 갱신하면 된다.
그렇다면 구간 합은 어떻게 구할까? 구간 합 역시 최말단 노드에서 시작해서 구간에 속하는 범위까지 구해 주면 된다. 만약 4~7구간 합을 구한다면 어떻게 될까? left는 4번째 데이터 인덱스를 가리키고, right는 7번째 데이터 인덱스를 가리키도록 한다. 그다음은 부모 노드로 올라가면서 누적합을 더해주면 된다.
이때 조심해야 할 부분이 있다. 현재 left는 4번째 데이터를 가리키고 있다. 하지만 부모 노드는 3~4 구간의 누적합이며 우리는 3구간은 필요가 없기 때문에 부모 노드에 올라갈 필요가 없다. 따라서 left의 누적합을 저장해 주고 +1을 통해 5번째 데이터를 가리키도록 한다. 만약 구간 합 범위가 3구간을 포함한다면 부모 노드로 바로 올라가면 된다.
마찬가지로 right도 현재 7번째 데이터를 가리키고 있다. 하지만 부모 노드는 7~8 구간의 누적합이며 우리는 8구간은 필요가 없기 때문에 부모 노드에 올라갈 필요가 없다. 따라서 right의 누적합을 저장해 주고 -1을 통해 6번째 데이터를 가리키도록 한다. 만약 구간 합 범위가 8구간을 포함한다면 부모 노드로 바로 올라간다.
이런 식으로 반복하면서 left < right를 만족할 때까지 진행하면 된다. 만약 left > right 면 최종 누적합을 반환하고, left = right 면 현재 left가 가리키는 누적합을 마지막으로 한 번 더 더해주고 최종 누적합을 반환한다.
다음은 Bottom-Up 방식의 세그먼트 트리를 JAVA로 구현한 코드이다. JAVA에는 2를 밑으로 가지는 log 함수가 없기 때문에 따로 만들어줘야 한다. 귀찮다면 넉넉하게 N * 4 정도의 트리 크기를 잡아주면 된다.
class Segment_Tree {
long[] tree;
int tree_Height;
int leafNode_startIndex;
public Segment_Tree(int N) {
tree_Height = baseLog(N, 2); //트리의 높이
leafNode_startIndex = 1 << (tree_Height - 1); //최말단 노드의 첫 번째 인덱스
tree = new long[1 << tree_Height];
//tree = new long[N << 2]; //트리의 높이 구하기 귀찮으면 대략 N의 4배
}
//base를 밑으로 가지는 log 함수
public int baseLog(double x, double base) {
return (int) Math.ceil(Math.log10(x) / Math.log10(base)) + 1;
}
//데이터 삽입 및 변경
public void update(int idx, long value) {
int pos = leafNode_startIndex + idx - 1;
tree[pos] = value;
while (pos > 1) {
pos /= 2;
tree[pos] = tree[pos * 2] + tree[pos * 2 + 1];
}
}
//구간 합 구하는 쿼리
public long query(int l, int r) {
long ret = 0;
int left = leafNode_startIndex + l - 1;
int right = leafNode_startIndex + r - 1;
while (left < right) {
//left가 가리키는 노드가 오른쪽 자식이면 현재 누적합을 더해주고 오른쪽으로 한칸 이동
if (left % 2 == 1) {
ret += tree[left++];
}
//right가 가리키는 노드가 왼쪽 자식이면 현재 누적합을 더해주고 왼쪽으로 한칸 이동
if (right % 2 == 0) {
ret += tree[right--];
}
//부모 노드로 올라감
left /= 2;
right /= 2;
}
//서로 같은 구간을 가리키면 마지막으로 현재 구간의 누적합을 더해줌
if (left == right) {
ret += tree[left];
}
return ret;
}
}
public class Blog {
public static void main(String[] args) {
Segment_Tree sg = new Segment_Tree(8);
sg.update(1, 1);
sg.update(2, 3);
sg.update(3, 5);
sg.update(4, 6);
sg.update(5, 8);
sg.update(6, 2);
sg.update(7, 6);
sg.update(8, 11);
System.out.println(sg.query(4, 7));
sg.update(5, 3);
System.out.println(sg.query(4, 7));
}
}
이번엔 재귀 함수를 이용한 Top-Down 방식을 알아보자. Bottom-Up 방식은 최말단 노드에서 시작하였다면 Top-Down 방식은 루트 노드에서 시작하여 최말단 노드까지 간 후 다시 올라오면서 구간의 누적합을 갱신해 주는 방식이다.
Bottom-Up 방식에서 본 것처럼 Top-Down 방식도 데이터를 삽입하거나 변경하는 방법은 동일하다. 루트 노드부터 시작하여 자신의 인덱스에 도달하면 값을 넣어준다. 그다음 다시 루트 노드까지 올라오면서 누적합을 갱신한다.
그렇다면 어떻게 자신의 인덱스를 찾아갈까? 재귀 호출 방식은 함수를 보며 이해해 보자.
//데이터 삽입 및 변경
public long update(int idx, long value, int node, int left, int right) {
//범위 밖의 구간은 갱신할 필요가 없음
if (idx < left || idx > right) return tree[node];
//계속해서 호출하다가 범위가 같은 경우 단말노드임
//단말노드에 value값을 넣고 다시 위로 올라가면서 단말 노드가 속한 범위 누적합 갱신
if (left == right) return tree[node] = value;
//절반으로 나눠서 자식들을 호출
//자식 노드들의 누적합을 부모 노드에 저장
int mid = (left + right) >> 1;
return tree[node] = update(idx, value, node * 2, left, mid) + update(idx, value, node * 2 + 1, mid + 1, right);
}
데이터를 삽입 및 변경하는 함수는 총 5개의 변수를 가진다. idx는 삽입할 데이터가 몇 번째 위치인지를 가리키고 value는 삽입할 데이터의 값, node는 현재 노드의 번호이다. left와 right는 현재 노드가 속한 구간을 뜻한다. 이 변수들이 어떻게 사용되는지 함수의 동작 과정을 통해 알아보자.
첫 시작은 루트 노드이기 때문에 node는 1이며, 루트 노드는 1~8 구간을 포함하기 때문에 left는 1, right는 8로 둔 후 3번 자리에 5의 값을 넣기 위해서 update(3, 5, 1, 1, 8) 함수를 호출한다.

left와 right가 다르기 때문에 현재 구간을 절반으로 나누어 자식 노드들을 호출한다. 완전 이진트리 형태이기 때문에 자식 노드의 번호는 부모 노드의 번호 * 2, 부모 노드의 번호 * 2 + 1이다. 1~8구간을 절반으로 나누면 1~4, 5~8이 된다. 이 값들을 통해 자식들을 호출한다.

1~4구간의 노드는 left와 right가 다르기 때문에 자식들을 호출한다. 5~8구간의 노드는 3번 인덱스를 벗어나는 구간이기 때문에 더 이상 자식들을 호출하지 않고 종료한다.

1~2구간의 노드는 3번 인덱스를 벗어나는 구간이기 때문에 더 이상 자식들을 호출하지 않고 종료한다. 3~4구간의 노드는 left와 right가 다르기 때문에 자식들을 호출한다.

3번 구간은 left와 right가 같기 때문에 올바른 위치이다. 따라서 10번 노드에 5를 저장하고 다시 루트 노드까지 역으로 올라가면서 3번 구간을 포함하는 구간의 누적합을 갱신해준다.

이러한 방식으로 단말 노드까지 간 후 다시 올라오면서 구간에 속하는 누적합들을 갱신해 준다.
그렇다면 구간 합을 어떻게 구할까? 3~5 구간 합을 구하는 과정을 함수의 동작 과정을 통해 살펴보자.
//구간 합 구하는 쿼리
public long query(int left, int right, int node, int nodeL, int nodeR) {
//범위 밖의 구간은 구할 필요가 없기 때문에 0을 리턴
if (right < nodeL || left > nodeR) return 0;
//현재 범위가 구하려는 구간에 속한다면 더이상 내려갈 필요가 없이 현재 누적합을 리턴
if (nodeL >= left && nodeR <= right) return tree[node];
//절반으로 나눠서 자식들을 호출
int mid = (nodeL + nodeR) >> 1;
return query(left, right, node * 2, nodeL, mid) + query(left, right, node * 2 + 1, mid + 1, nodeR);
}
구간 합을 구하는 함수는 총 5개의 변수를 가진다. left와 right는 구해야 할 구간을 의미한다. node는 현재 노드의 번호를 뜻하고 nodeL과 nodeR은 현재 노드가 속한 범위를 뜻한다. 이 변수들이 어떻게 사용되는지 알아보자.
3~5구간 합을 구하기 위해 query(3, 5, 1, 1, 8)을 호출한다.

1~8 구간은 3~5 구간을 넘어가기 때문에 현재 구간을 절반으로 나누어 자식 노드들을 호출한다. 1~8 구간을 절반으로 나누면 1~4, 5~8이 된다. 이 값들을 통해 자식들을 호출한다.

1~4구간은 3~5구간을 넘어가기 때문에 자식 노드들을 호출한다. 5~8구간 역시 마찬가지로 3~5구간을 넘어가기 때문에 자식 노드들을 호출한다.
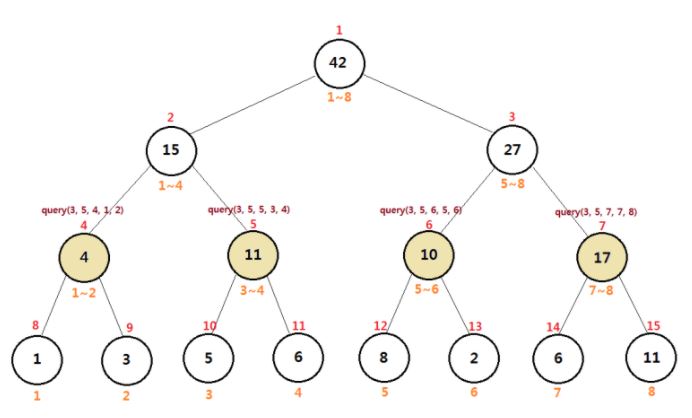
1~구간은 구할 필요가 없는 구간이기 때문에 0을 반환하며 함수를 종료한다. 3~4구간은 구해야하는 3~5구간에 속하기 때문에 더 이상 내려갈 필요가 없이 현재 노드의 누적합 11을 반환하고 루트 노드까지 올라간다.
5~6구간은 3~5구간을 넘어가기 때문에 자식 노드들을 호출한다. 7~8 구간은 구할 필요가 없는 구간이기 때문에 0을 반환하며 함수를 종료한다.

5구간은 구해야하는 3~5구간에 속하기 때문에 현재 노드의 누적합 8을 반환하고 루트 노드까지 올라간다. 6구간은 3~5구간에 속하지 않기 때문에 0을 반환하며 함수를 종료한다.

최종적으로 11 + 8 = 19를 루트 노드까지 반환하여 3~5 구간의 누적합을 구하게 된다.
재귀 호출 방식은 단말 노드까지 갔다가 다시 루트 노드로 올라오는 2번의 이동 과정으로 반복문을 이용한 방식보다 시간은 느리지만 이를 응용한 복잡한 세그먼트 트리를 구현하기에 용이한 확장성이 뛰어난 장점이 있다.
재귀 호출 방식을 JAVA로 구현한 코드는 다음과 같다.
class Segment_Tree {
long[] tree;
int tree_Height;
public Segment_Tree(int N) {
tree_Height = baseLog(N, 2); //트리의 높이
tree = new long[1 << tree_Height];
//tree = new long[N << 2]; //트리의 높이 구하기 귀찮으면 대략 N의 4배
}
//base를 밑으로 가지는 log 함수
public int baseLog(double x, double base) {
return (int) Math.ceil(Math.log10(x) / Math.log10(base)) + 1;
}
//데이터 삽입 및 변경
public long update(int idx, long value, int node, int left, int right) {
//범위 밖의 구간은 갱신할 필요가 없음
if (idx < left || idx > right) return tree[node];
//계속해서 호출하다가 범위가 같은 경우 단말노드임
//단말노드에 value값을 넣고 다시 위로 올라가면서 단말 노드가 속한 범위 누적합 갱신
if (left == right) return tree[node] = value;
//절반으로 나눠서 자식들을 호출
int mid = (left + right) >> 1;
return tree[node] = update(idx, value, node * 2, left, mid) + update(idx, value, node * 2 + 1, mid + 1, right);
}
//구간 합 구하는 쿼리
public long query(int left, int right, int node, int nodeL, int nodeR) {
//범위 밖의 구간은 구할 필요가 없기 때문에 0을 리턴
if (right < nodeL || left > nodeR) return 0;
//현재 범위가 구하려는 구간에 속한다면 더이상 내려갈 필요가 없이 현재 누적합을 리턴
if (nodeL >= left && nodeR <= right) return tree[node];
//절반으로 나눠서 자식들을 호출
int mid = (nodeL + nodeR) >> 1;
return query(left, right, node * 2, nodeL, mid) + query(left, right, node * 2 + 1, mid + 1, nodeR);
}
}
public class Blog {
public static void main(String[] args) {
Segment_Tree sg = new Segment_Tree(8);
sg.update(1, 1, 1, 1, 8);
sg.update(2, 3, 1, 1, 8);
sg.update(3, 5, 1, 1, 8);
sg.update(4, 6, 1, 1, 8);
sg.update(5, 8, 1, 1, 8);
sg.update(6, 2, 1, 1, 8);
sg.update(7, 6, 1, 1, 8);
sg.update(8, 11, 1, 1, 8);
System.out.println(sg.query(3, 5, 1, 1, 8));
}
}
'Computer Science > 자료구조' 카테고리의 다른 글
| 트라이(Trie) (0) | 2021.06.30 |
|---|---|
| 맵(Map) & 셋(Set) (0) | 2021.06.30 |
| 해싱 : Hashing (0) | 2021.06.30 |
| 그래프(Graph) (0) | 2021.06.30 |
| 우선순위 큐(Priority Queue) (0) | 2021.06.30 |



댓글