이번에 배워볼 자료구조는 트라이(Trie) 자료구조이다. 요즘 코딩 테스트에서 트라이를 이용하여 푸는 문제들이 자주 등장하여 한번 짚고 넘어가려 한다.
트라이를 공부하기 전에 트라이가 왜 필요한지 알아보자. 현재 "abbce", "acd", "bfgaa", abbga", "acde"의 문자열을 포함하는 리스트가 존재한다고 하자.
만약 "bfgaa"라는 문자열이 리스트 내에 존재 유무를 파악하기 위해선 우리는 리스트에 들어있는 문자열들을 비교해봐야 한다.
리스트 내에 찾고자 하는 문자열이 존재하지 않는 최악의 경우 모든 문자열을 비교해야 하기 때문에 O(리스트에 들어있는 모든 문자열의 총 길이) 만큼의 시간 복잡도가 들게 된다. 이는 문자열 간의 불필요한 비교를 계속 진행하기 때문에 상당히 비효율적인 방법이다.
이를 개선할 방법은 없을까? 바로 트라이 자료구조를 이용하는 것이다. 트라이는 트리를 활용한 자료구조로써 문자열 집합을 표현하고 찾고자 하는 문자열의 길이가 N 일 때 O(N)이라는 빠른 시간에 문자열이 존재하는지 확인할 수 있는 자료구조이다.
트라이 자료구조는 글보단 그림으로 보는 것이 이해하기가 쉬울 것이다.
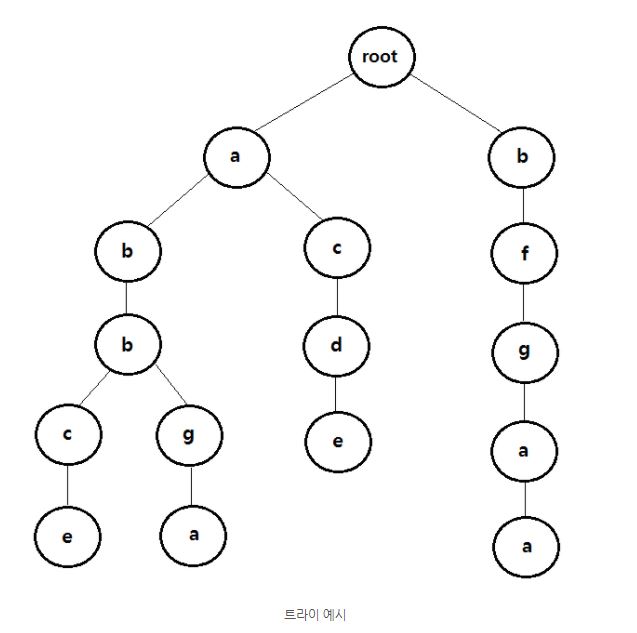
위 그림은 위의 문자열들을 모두 삽입한 트라이 자료구조이다. 자세히 보면 루트 정점을 제외한 각 정점들은 자신을 대표하는 문자 한 개를 지니고 있음을 알 수 있다.
그렇다면 문자열을 트라이에 어떻게 삽입할까? 트라이는 먼저 root라는 아무런 값을 가지지 않는 정점 한 개를 가지면서 시작한다.
"abbce"라는 문자열을 트라이에 삽입한다면 먼저 root부터 시작하여 root의 자식 중 'a'를 가지는 자식이 존재한다면 자식으로 진입하고 존재하지 않는다면 'a'를 가지는 새로운 자식을 생성한 후 진입해 준다. 이런 식으로 문자열의 끝까지 반복하게 되면 "abbce"를 가지는 트라이를 만들 수 있다.

이번에는 "abbga"라는 문자열을 트라이에 삽입해보도록 하자. root부터 시작하여 'a', 'b', 'b'까지는 이미 해당 문자를 가지는 정점이 존재하기 때문에 자식을 생성할 필요 없이 바로 진입할 것이다.
'b'의 자식들중 'g'를 가지는 정점이 존재하지 않기 때문에 'g'를 가지는 정점을 생성해준다. 생성된 'g;를 가지는 정점 또한 'a'를 가지는 자식이 존재하지 않기 때문에 'a'를 가지는 정점을 생성해준다.
이런 식으로 주어진 문자열을 삽입하여 트라이를 구성할 수 있다.

그렇다면 문자열의 존재 유무는 어떤 식으로 판단할까? 트라이에서 "bfgaa"라는 문자열이 존재하는지 탐색한다면 root부터 시작하여 'b'-'f'-'g'-'a'-'a', 문자열의 길이만큼만 자식이 존재하는지 확인한다면 해당 문자열의 존재 유무를 판단할 수 있다.
"acfe"라는 문자열을 탐색한다면 root-'a'-'c'까지는 정점이 존재하지만 'c'의 자식들 중 'f'를 가지는 정점이 존재하지 않기 때문에 해당 문자열은 존재하지 않는다고 판단할 수 있다.

그렇다면 트라이는 단점은 없을까? 트라이는 효율적인 시간 복잡도를 가진다는 것을 알 수 있다. 하지만 공간 복잡도(메모리) 부분에서는 상당히 부담이 크다.
자세히 보면 각 정점들은 자신을 대표하는 문자 한 개와 자식들을 항상 지니고 있는 것을 알 수 있다. 대충 짐작했을 테지만 자식의 총개수는 사용할 문자의 총개수이다.
간단하게 영어 소문자만 사용한다고 했을 경우 각정점들마다 'a'부터 'z'까지 총 26개의 자식들을 지녀야 한다는 것을 의미한다.
결국 트라이의 공간 복잡도는 O(정점의 총 개수 x 사용할 문자의 개수)이다. 이는 사용하지 않는 문자에도 불구하고 정점이 생성될 때마다 자식을 지녀야 하기 때문에 메모리를 낭비하게 된다. 따라서 상황에 맞게 트라이 자료구조를 활용해야 한다.
다음은 영어 소문자만 가지는 트라이를 Java로 간단하게 구현한 코드이다.
class Node {
char data;
Node[] child;
public Node() {
child = new Node[26];
}
public Node(char data) {
this.data = data;
child = new Node[26]; //'a'부터 'z'까지 총 26개의 자식 노드를 생성
}
}
class Trie {
Node root;
public Trie() {
root = new Node(); //root 노드 생성
}
public void make_Trie(Node root, int pos, String input) {
//문자열을 다 삽입했기 때문에 종료
if (pos == input.length()) return;
char ch = input.charAt(pos);
int index = (int)ch - 97; //'a' 아스키 코드값이 97이기 때문에 -97해줘서 0으로 만들어줌
//root의 자식들중 ch를 가지는 자식이 없다면 자식을 하나 생성하고 가리키도록 함
if (root.child[index] == null) {
Node node = new Node(ch);
root.child[index] = node;
}
//자식 노드로 진입
make_Trie(root.child[index], pos + 1, input);
}
public void isExist(Node root, int pos, String input) {
if (pos == input.length()) {
System.out.println("트라이에 " + input + " 문자열 존재 O");
return;
}
char ch = input.charAt(pos);
int index = (int)ch - 97; //'a' 아스키 코드값이 97이기 때문에 -97해줘서 0으로 만들어줌
//ch를 가지는 자식 노드가 존재하지 않는다면
if (root.child[index] == null) {
System.out.println("트라이에 " + input + " 문자열 존재 X");
return;
}
//자식 노드로 진입
isExist(root.child[index], pos + 1, input);
}
}
public class Blog {
public static void main(String[] args) {
Trie trie = new Trie();
trie.make_Trie(trie.root, 0, "abbce");
trie.make_Trie(trie.root, 0, "acd");
trie.make_Trie(trie.root, 0, "bfgaa");
trie.make_Trie(trie.root, 0, "abbga");
trie.make_Trie(trie.root, 0, "acde");
trie.isExist(trie.root, 0, "bfgaa");;
trie.isExist(trie.root, 0, "acfe");
}
}
'Computer Science > 자료구조' 카테고리의 다른 글
| 세그먼트 트리(Segment Tree) (0) | 2021.06.30 |
|---|---|
| 맵(Map) & 셋(Set) (0) | 2021.06.30 |
| 해싱 : Hashing (0) | 2021.06.30 |
| 그래프(Graph) (0) | 2021.06.30 |
| 우선순위 큐(Priority Queue) (0) | 2021.06.30 |



댓글