반응형
이번에 배워볼 정렬 알고리즘은 합병 정렬(Merge Sort)이다.
이전까지 배운 정렬들은 최악의 경우 시간 복잡도가 O(N^2)이지만, 합병 정렬은 이와 다르게 최선, 평균, 최악 모든 경우가 O(N logN)의 시간 복잡도를 가지는 빠른 정렬 알고리즘이다.
합병 정렬은 하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다.
합병 정렬은 분할 정복(Divide and Conquer) 방법에 바탕을 두고 있다. 분할 정복 방법은 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.
합병 정렬은 다음의 단계들로 이루어진다.
- 분할(Divide) : 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
- 정복(conquer) : 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.
- 결합(Combine) : 정렬된 부분 배열들을 하나의 배열에 합병한다.
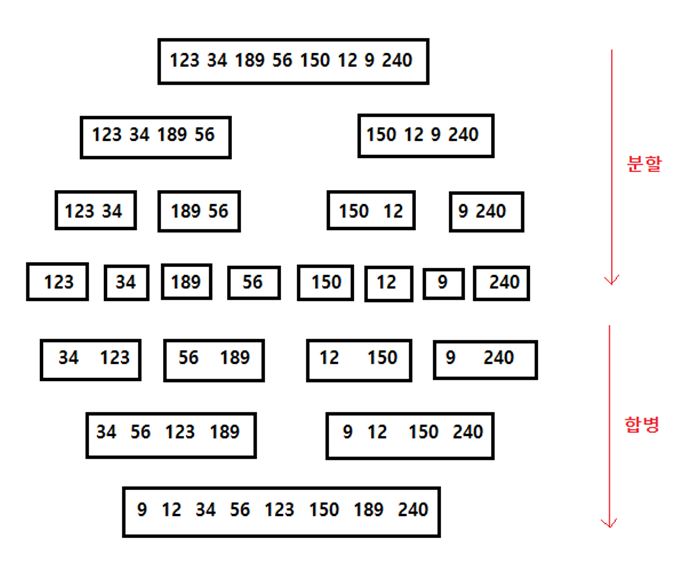
그림에서 분할 과정을 보면 리스트의 요소들이 1개가 될 때까지 분할한다. 여기까지는 이해하기가 쉬울 것이다. 더 이상 분할할 수 없는 단계까지 다다르면 분할된 원소들을 다시 합병해야 한다.
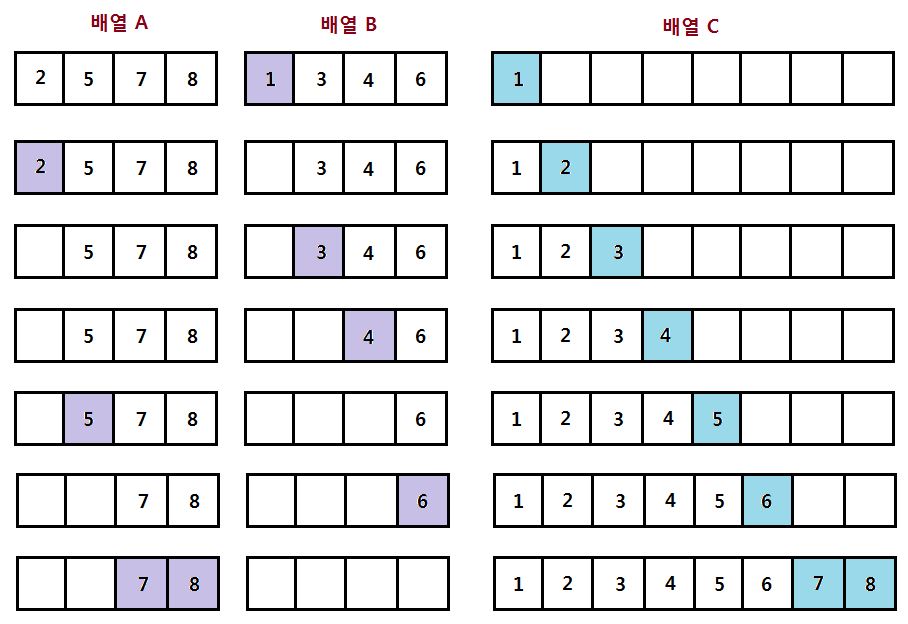
합병을 하기 위해선 추가적인 리스트를 필요로 한다. 2개의 정렬된 리스트의 요소들을 처음부터 하나씩 비교하여 2개의 리스트의 요소 중에서 더 작은 요소를 새로운 리스트로 옮긴다. 이 과정을 반복하여 하나의 리스트를 끝까지 옮기게 되면, 남은 리스트의 요소들을 새로운 리스트에 옮겨주면 한 번의 합병 과정이 끝이 난다.
합병 정렬(Merge Sort)의 시간 복잡도는 O(N logN)이다.
합병 정렬을 Java로 구현한 코드는 다음과 같다.
public class Main {
static int[] sort; //새로운 리스트
public static void main(String[] args) {
int[] arr = {2,5,7,8,1,3,4,6};
sort = new int[arr.length];
merge_Sort(0, arr.length - 1, arr);
for (int a : arr) {
System.out.print(a+" ");
}
}
public static void merge_Sort(int left, int right, int[] arr) {
if (left < right) {
int mid = (left + right) >> 1;
//배열의 원소가 1개일때까지 분할한다.
merge_Sort(left, mid, arr);
merge_Sort(mid + 1, right, arr);
//분할된 배열들을 정렬하면서 병합한다.
merge(left, mid, right, arr);
}
}
public static void merge(int left, int mid, int right, int[] arr) {
int i = left;
int j = mid + 1;
int k = left;
//2개의 배열중 한개를 끝까지 새로운 배열에 옮기기 전까지
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
sort[k++] = arr[i++];
} else {
sort[k++] = arr[j++];
}
}
//남은 한개의 배열의 요소들을 새로운 배열에 옮겨줌
if (i > mid) {
for (; j <= right; ++j) {
sort[k++] = arr[j];
}
} else {
for (; i <= mid; ++i) {
sort[k++] = arr[i];
}
}
//정렬한 배열을 다시 원본 배열에 옮겨줌
for (int start = left; start <= right; ++start) {
arr[start] = sort[start];
}
}
}반응형
'Computer Science > 알고리즘' 카테고리의 다른 글
| 힙 정렬(Heap Sort) (0) | 2021.07.01 |
|---|---|
| 퀵 정렬(Quick Sort) (0) | 2021.07.01 |
| 버블 정렬(Bubble Sort) (0) | 2021.07.01 |
| 삽입 정렬(Insertion Sort) (0) | 2021.07.01 |
| 선택 정렬(Selection Sort) (0) | 2021.07.01 |




댓글